
科技改变生活 · 科技引领未来

科技改变生活 · 科技引领未来
证明√2是无理数用到初三学到的反证法即可轻松证明,包括初一的数学书也拓展到了这一内容,具体为:
假设√2为有理数,那么√2=a/b(a、b为整数且a、b互质),∴√2a=b.∴2a2=b2①.∴b2为偶数.∵b为整数,∴b为偶数.令b=2s,则s为整数,代入①式得2a2=(2s)2,∴a2=2s2.同理可得a为偶数,∴a、b不互质,从而假设有误.即:√2不是有理数.
√4=2,同上述一样,假设√4=a/b,可以得到4a2=b2,∴b为4的倍数,然后得出a、b都为4的倍数,从而2不是有理数.
其实,假设√4=a/b(a、b为整数且互质),只能得出b2为4的倍数,从而b为2的倍数(b不一定是4的倍数),令b=2s,能得出4a2=(2s)2,无法推出a为偶数.
虽然数学有一定的难度,但只要能细细地去揣摩它的奥妙,数学就会十分有趣.
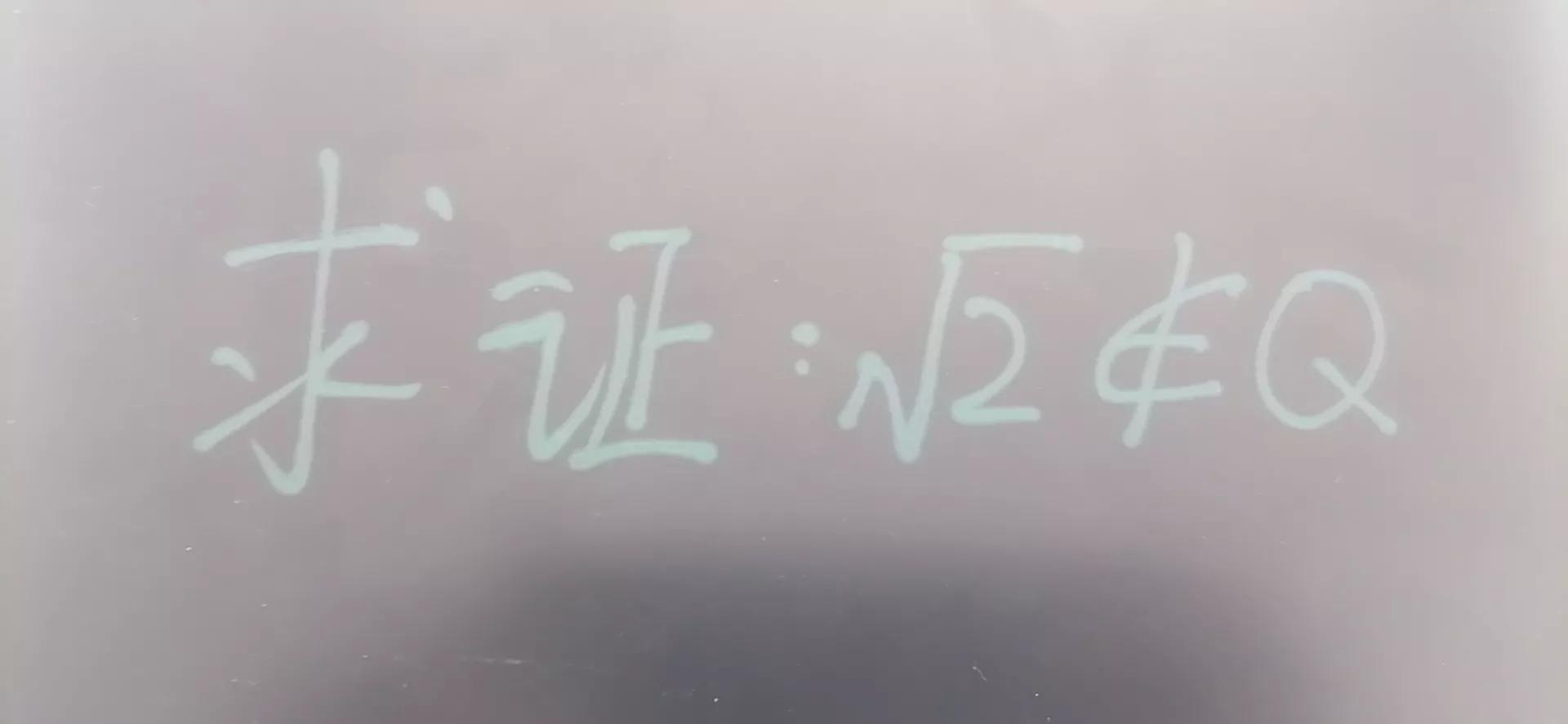

金阳远
